even function example | even vs odd function

WeightWatchers is the #1 doctor-recommended weight-loss program†. We help you lose weight and build healthy habits, one small step at a time. Fad weight-loss diets can be restrictive, and rarely work long term. We have .

even function example*******The important properties of even functions are listed below: 1. For any function f(x), f(x) + f(−x) is an even function. 2. The sum or difference of two even functions is even. 3. The multiple of an even function is again an even function. 4. The product or division of two even functions is even. For . Tingnan ang higit paSome of the examples of even functions include the following. 1. cos x since cos(-x) = cos x 2. x2, x4, x6, x8,., i.e. xnis an even function when n is an even integer 3. |x| 4. . Tingnan ang higit pa

The formula of an even function is simply the expression that helps to identify whether a function is even. Function f(x) = even if f( . Tingnan ang higit pa

Even function and odd function can be defined as given below: Example of Even Function and Odd Function The graph below shows both even and odd functions. Tingnan ang higit paA function is an even function if f of x is equal to f of −x for all the values of x. This means that the function is the same for the positive x-axis and the negative x-axis, or .Even Functions. A function is "even" when: f (x) = f (−x) for all x. In other words there is symmetry about the y-axis (like a reflection): This is the curve f (x) = x2+1. They are called "even" functions because the .Even and odd functions are named based on the fact that the power function f(x) = x n is an even function, if n is even, and f(x) is an odd function if n is odd. Let us explore other even and odd functions and .

Even function definition. Even functions are functions that return the same expression for both x and -x. This means that if f (x) is an even function when f (-x) = f (x). An even . Understand what an even function is. Explore what an even function looks like using a graph. Learn about the symmetry of an even function with examples. .

If f of negative x is equal to the function again, then we're dealing with an even function. If we evaluate f of negative x, instead of getting the function, we get the . If you evaluate j at some value-- so let's say j of a. And if you evaluate that j at the negative of that value, and if these two things are the negative of each other, then my function is odd. If these two things were the same-- if they didn't have this negative .

Examples of even functions include 1 (or, in general, any constant function), |x|, cosx, x^2, and e^(-x^2). An even function times an odd function is odd, . Even functions are symmetrical about the y-axis: f(x)=f(-x). Odd functions are symmetrical about the x- and y-axis: f(x)=-f(-x). Let's use these definitions to .

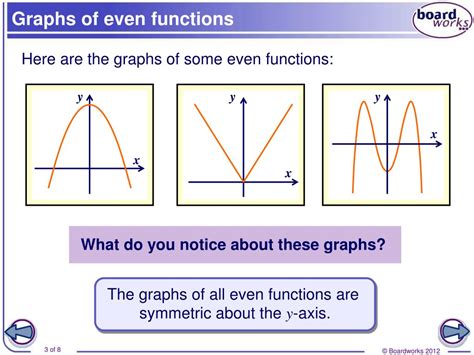
An even function is symmetric about the y-axis of the coordinate plane while an odd function is symmetric about the origin. Most functions are neither even nor odd. . Example. Determine whether f(x) = 5x 5 - 4x .

An even function is symmetric about the y-axis of the coordinate plane while an odd function is symmetric about the origin. Most functions are neither even nor odd. . Example. Determine whether f(x) = 5x 5 - 4x .

even function exampleAn even function is symmetric about the y-axis of the coordinate plane while an odd function is symmetric about the origin. Most functions are neither even nor odd. . Example. Determine whether f(x) = 5x 5 - 4x .

It is said to be even if f ( − x) = f ( x) for every x in the domain of f. An odd function, in turn, is the one that satisfies the property f ( − x) = − f ( x) for every x-value. If none of . The function is odd if f(x) = -f(-x).The rule of a thumb might be that if a function doesn't intercepts y at the origin, then it can't be odd, and y = -x + 4 is shifted up and has y-intercept at 4. .even vs odd functionSo, a function can never be symmetrical around the x-axis. Just remember: symmetry around x-axis ≠ function. To answer your second question, "even" and "odd" functions are named for the exponent in this power function: f (x) = xⁿ. - if n is an even integer, then f (x) is an "even" function. - if n is an odd integer, then f (x) is an "odd .A function f f is called an even function if. f(x)= f(−x) f ( x) = f ( − x) for all x x in the domain of f. f. In other words, a function is even if performing a reflection about the y y -axis does not change the graph of the function. To help remember the definition of an even function, notice that the example of an even function we gave . If any given function follows the above rule, it is said to be an even function. The graph of any even function is symmetric to the y-axis, i.e. it forms a mirror image. Solved Examples. It is essential to go through some examples to understand the above-mentioned points properly. Some illustrations on how to know if a function is .Examples of even functions. To have a better understanding of even functions, it is advisable to practice some problems. For the function. h ( x) = 6 x 6 - 4 x 4 + 2 x 2 - 1. Determine if it is an even function. Plot the graph and pick any two points to prove that it is or is not an even function. Solution:

even function example even vs odd function9. Even and Odd Functions. By M. Bourne. Even Functions. A function `y = f(t)` is said to be even if. f(−t) = f(t). for all values of t.. The graph of an even function is always symmetrical about the vertical axis (that is, we have a mirror image through the y-axis).. The waveforms shown below represent even functions:. Cosine curve

Mandaluyong business permit renewal 2024 gives individuals the opportunity to renew their mayor’s permits every year from January 1 through January 20. Every enterprise must renew their permits regardless of their registration date with the Department of Trade and Industry (DTI), Securities and Exchange Commission (SEC), .

even function example|even vs odd function